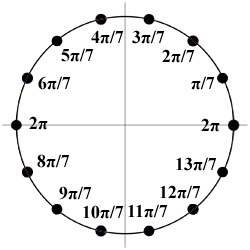
This question comes about from a posting in one of the math forums I hang out on. 

Typically, when dealing with trig functions, we see “nice” values for sines and cosines… and by that I mean it’s possible to obtain exact values for them.  For example, stuff like π/6, π/4, π/3, π/2, or multiples thereof.  But what about the the expression is a value we can’t obtain an exact value for?  For example, what consider the following:

cos(2π/7) +cos(4π/7) + cos(8π/7) = -1/2

How in the world can this be proved (or not)?  We don’t even have a value for cos(π/7), let alone most multiples of it.  What do we do? 

The best way to prove anything will be to see of we can get terms to cancel.  That is, can we reduce the complexity of the equation down to something that’s always true?  For example, cos(π/7)= cos(π/7)?  Or even something that’s not true, such as cos(3π/7)=0.  However we can get to something like this, that will prove – or disprove – our equation. 

That said, let’s try to simplify the left side.  In other words, we want to be able to try and collect like terms. 

For starters, there is a trigonometric identity that says:
sin(x)cos(y) = (1/2)[(sin(x+y)+sin(x-y)]

Let's multiply both sides of the equation by sin(π/7):
sin(π/7)cos(2π/7) + sin(π/7)cos(4π/7) + sin(π/7)cos(6π/7) = -1/2

Now, we apply the identity above:
(1/2)[sin(π/7+2π/7) + sin(π/7-2π/7)] + (1/2)[sin(π/7+4π/7) + sin(π/7-4π/7)]
+ (1/2)[sin(π/7+8π/7) + sin(π/7-8π/7)] = -(1/2)sin(π/7)

We can multiply both sides by 2 and simplify the terms a bit:
[sin(3π/7) + sin(-π/7)] + [sin(5π/7) + sin(-3π/7)] + [sin(9π/7) + sin(-7π/7)] = -sin(π/7)

Further simplifying:
sin(3π/7) - sin(π/7) + sin(5π/7) - sin(3π/7) + sin(9π/7) - sin(7π/7) = -sin(π/7)

Now, we can collect like terms:
sin(5π/7) + sin(9π/7) - sin(7π/7) = 0

But sin(7π/7) = 0:
sin(5π/7) + sin(9π/7) = 0

That’s a lot simpler.  But what does sin(5π/7) + sin(9π/7) equal, anyway?  Do they sum to zero? 

Maybe the following diagram will help: 

Each point has the coordinates (sin<angle>, cos<angle>).  This means a couple of things.  We can see that the sine of 5π/7 is a positive number.  In a similar manner, the sine of 9π/7 is a negative number.  Further, since they are the same distance from π, they are the same quantity, except that one is positive and one is negative.  In other words, by consideration of where the angles are, we can deduce that they in fact add to zero.  We have thus confirmed that

sin(5π/7) + sin(9π/7) = 0

is a true statement!  Thus, the equation as presented holds true.    

By the way, the last term of the left half of the equation can be cos(6π/7), and the equality still holds true.  Why? 

Consider our diagram again.  We know that cos(6π/7) and cos(8π/7) are also the same distance from π.  We don’t know that value, but in the case of the cosine function we know both values are negative.  Thus, whether we say:

cos(2π/7) +cos(4π/7) + cos(8π/7) = -1/2

or

cos(2π/7) +cos(4π/7) + cos(6π/7) = -1/2

we have a true statement, because cos(6π/7) = cos(8π/7).  

This question is actually a pretty clever math poser that was asked on Facebook.  You can see the question on Facebook here, and it's a fun little brain exercise to see what you think the answer is before reading on. As of this post, it's been answered by almost five million people!  The possible answers are 0, 14, 16, and 17.   Which answer is right?  

This question relies on two things: 
1.  How observant you are
2.  Knowledge of mathematical priority (or knowing what is supposed to be done first).  

To start, there are seventeen 1's in the question.  Summing all of them would give 17.  But as can be seen on the end, the last 1 is multiplied by zero.  So we can eliminate 17 as an answer.  

So the question now is: do we do that 1x0 before all that addition, or last?  

In math, the order of operators is as follows: 
Always evaluate anything in parenthesis first
Then, do multiplication or division from left to right
Lastly, perform addition or subtraction from left to right
So, we need to evaluate the 1x0 first.  Doing so leaves sixteen 1's.  So is the answer 16?  

Nope!  This is where the problem tests how observant you are.  Look at the eleventh 1 in the problem: it is actually subtracted, not added.  Thus, we have sixteen 1's, fifteen on which are positive and one of which is negative, which will sum to 14.  Doing the math from left to right gives a running total this way:  
1,2,3,4,5,6,7,8,9,10,9,10,11,12,13,14,14
Either way, the answer is 14.  

It's surprising that about half of all the answers are 0.  In fact, only about a third of all responders got the answer correct!  Hey... anyone need some math tutoring? :-)

We can add, subtract, multiply and divide any two numbers we want, right?  Well... almost.  The one weird exception is division and zero: we simply cannot divide by zero.  Why is that?  

Consider what we are asking with that question.  If we say, for instance, x divided by zero or x/0, we are asking:

x/0 = ?

We get that solution by multiplying both sides of the equation by zero:

x = 0 * ?

If x is zero, there is no single solution.... it means ? can be any real number!  
If x is not zero, ? has to be a number that, when multiplied by zero, is not zero!  If you can find a real number that satisfies that qualification, let me know... but I'm not holding my breath.  
Anyway, we wind up with an infinite number of answers, or we wind up with an impossible answer.  Either way, it just doesn't work.  

Some people maintain that anything over zero is infinity, reasoning that the smaller the denominator gets, the larger the fraction.  For instance:

1 / 1 = 1
1 / 0.1 = 10
1 / 0.01 = 100
1 / 0.001 = 1,000
1 / 0.0001 = 10,000

and so on.  The reasoning goes that by extrapolating that out, we would get

1 / 0 = ∞

And since this could apply for any non-zero numerator, it is then tempting to say that 

x/0 = ∞


Seems reasonable enough.  Problem is, we could then do some fuzzy math along the lines of

since 1 / 0 = ∞
and 2 / 0 = ∞
and ∞ = ∞

one could say

1 / 0 = 2 / 0

And, multiplying both sides by zero, we'd get

1 = 2

Which isn't true.  It proves that our initial definition 
x/0 = ∞
is a fallacy.  It just doesn't work.  

After all, think of the definition of division.  It's taking a quantity and dividing it into equal parts.  Can you imagine taking six apples and dividing them among no people?  Unless you are stuck in the Matrix somewhere, you answer will invariably be: "you can't."  And that's really why division by zero is prohibited... you just can't do it.  

Welcome to the mathbyte math blog!  On here, you'll see little tidbits - about one a week or so - about all sorts of topics related to computers.  The topics could be anything from interesting math facts, to not-so-well-known rules of math, or even the occasional tricky homework problem.  I'll also discuss any questions you might have, about concepts or even a question regarding a homework problem.  Feel free to email about any math-related topic and I'll try and get it on the blog!